二叉树遍历有 前/中/后序 + 层次,那么树和森林的遍历是怎么进行的呢?其与对应的二叉树的遍历有什么联系呢?
树的遍历
对于一棵树,根结点 + 子树(从左到右)(子树又为 根结点 + 子树)。因此有两种访问:
1、先访问根,再依次访问子树 – 先根遍历
2、先依次访问子树,再访问根 – 后根遍历
注意:没有中根遍历了哦,因为树的度可能超过2,不遵循左根右的中根遍历如图:
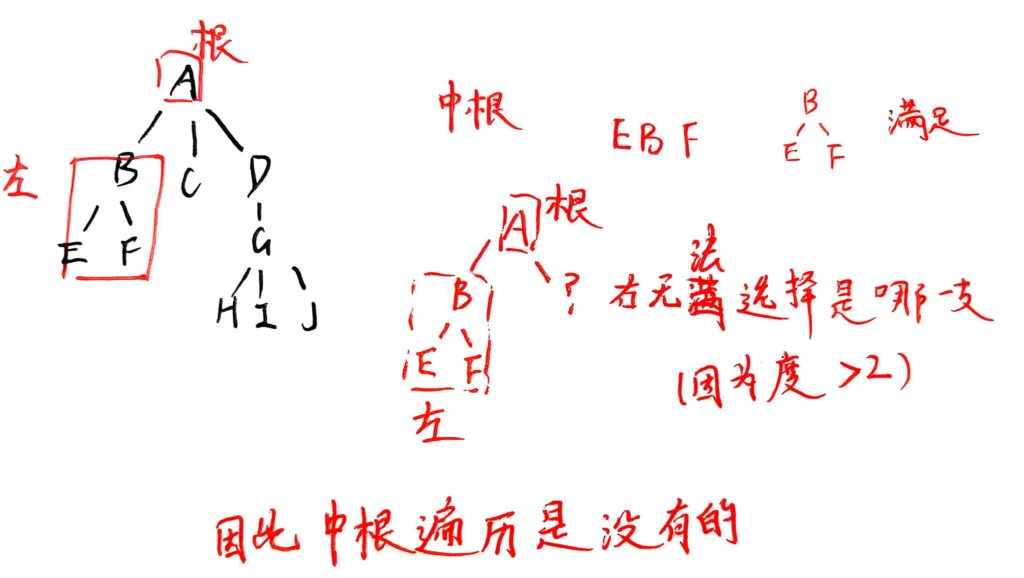
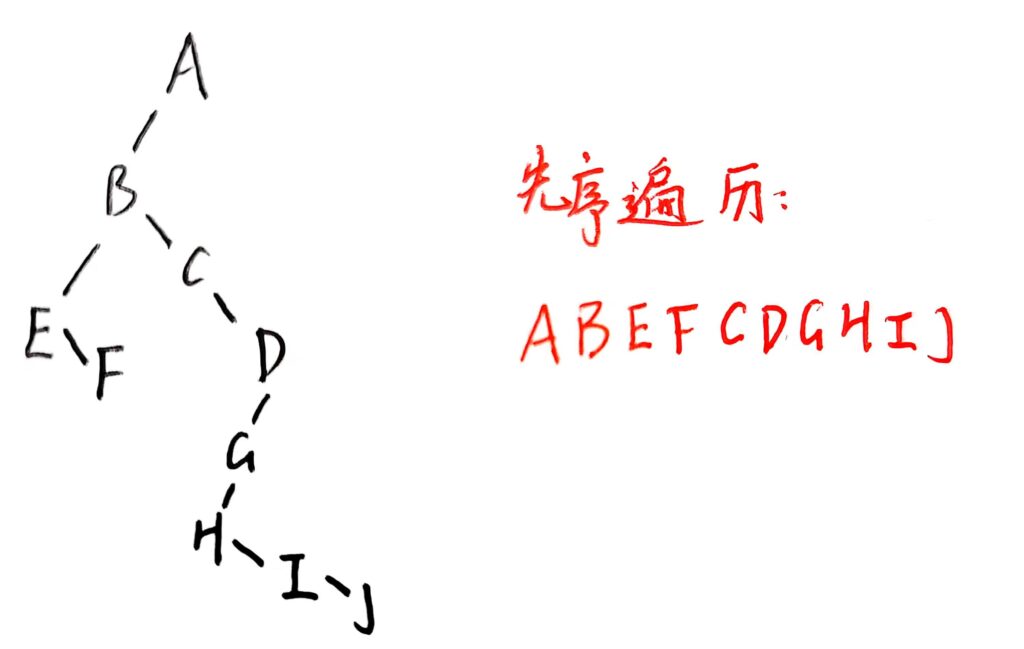
先根遍历

树的先根遍历和其对应的二叉树的先序遍历序列是一样的。如图:
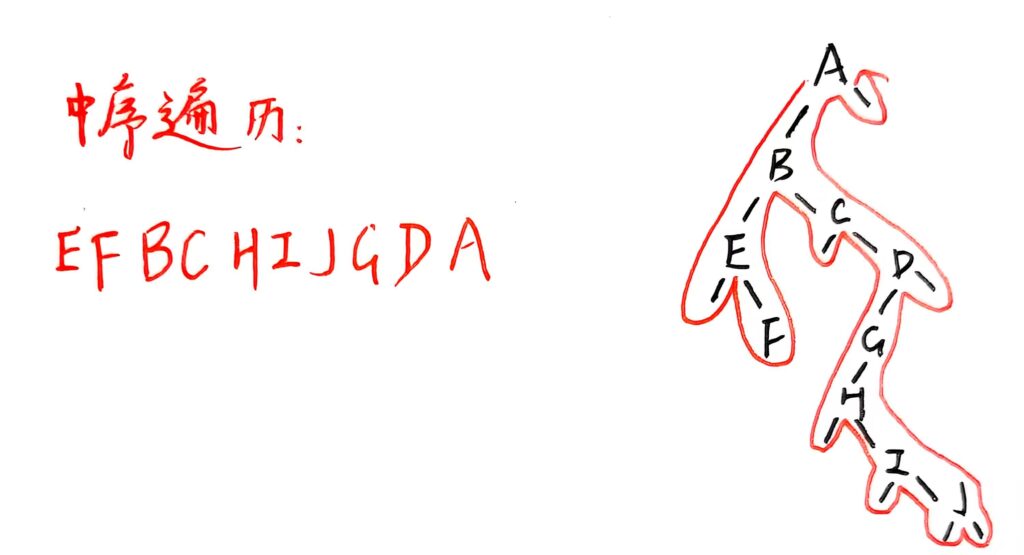
后根遍历

树的后根遍历与其对应的二叉树的中序遍历序列一致。如图:
森林的遍历
森林是如何遍历的呢? 对森林中的各棵树从左到右进行前根遍历 或者 后根遍历 即得到 森林的先序遍历和中序遍历。
先序遍历
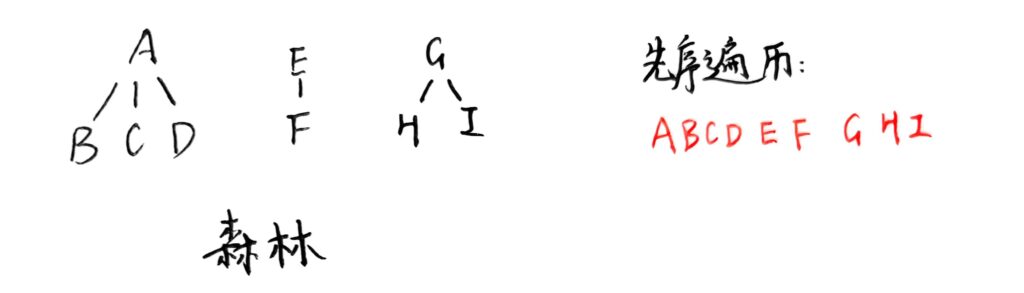
森林的先序遍历和其对应的二叉树的先序遍历序列一致。如图:

中序遍历(也可以称为后序遍历)
该遍历由于理解角度不同,称为森林的中序遍历或者森林的后序遍历都行
1、将第一棵树的子树看作左,将第一棵树的根节点看作根,将剩余树看作右,则可以理解为根的中序遍历。
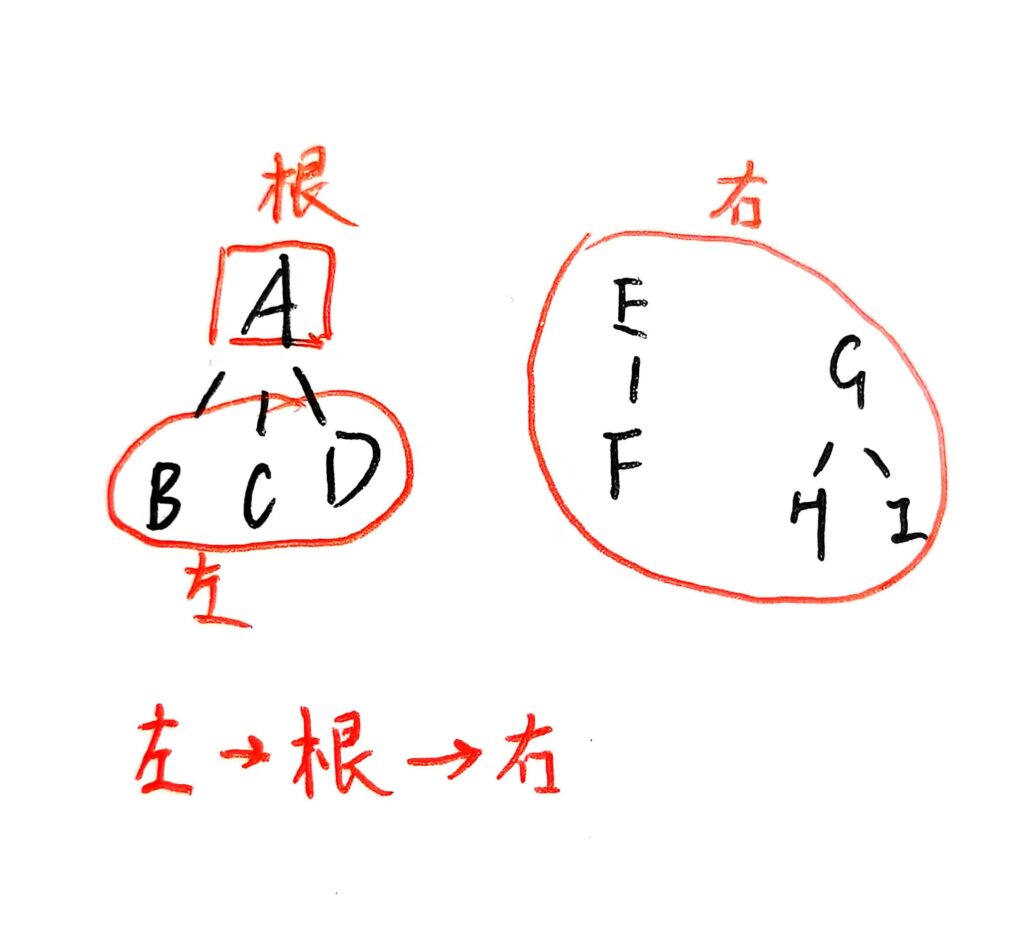
2、由于是对森林的每棵树作后根遍历得到,因此称为森林的后序遍历也理所当然(毕竟每棵树的根都是最后遍历的)。
不管从何角度理解,最终的森林的中(后)序遍历是一致的,阿Q在这就理解为森林的中序遍历吧。

森林的中序遍历和其对应的二叉树的中序遍历序列一致。如图:

总结
- 树的先根遍历和其对应的二叉树的先序遍历一致;
- 树的后根遍历和其对应的二叉树的中序遍历一致;
- 森林的先序遍历和其对应的二叉树的先序遍历一致;
- 森林的中序遍历和其对应的二叉树的中序遍历一致。
因此:对树和森林的遍历 可以将其转化为相应的二叉树再进行遍历。
阿Q:掌握二叉树,即掌握了森林和树。
评论