阿Q的感悟
阿Q从2月10日起都是看书自学的,但是在 3月5日这天遇到了不定积分,阿Q自己看没怎么明白,于是去B站找了不定积分课程,在听了凯哥讲解有理函数积分后倍感还是要针对性地去听课 + 整理,不然自学掌握的只能是冰山一角。
接下来的数学学习之路要改正一下,先自学一遍张宇本讲内容,然后去搜相应的课程,看看自己漏了多少知识,然后补上。
2025考研数学大纲
高数
线性代数
概率论与数理统计
心路历程
25-3-16 一元函数积分学
阿Q之前一直都对积分学有很浅显的认知,对不定积分,定积分,变限积分和反常积分的概念十分混乱。
阿Q在看完了定积分和不定积分的计算 后 从头再看概念,有种全新的视角,迫不及待地想记录下来。
阿Q的新视觉有:
1、目前对整个高数的看法(阿Q表述不出来,在ds小姐帮助下才描绘出语言):
- 微分学的视角:从函数到变化(预测未来)
- 核心:通过已知函数(或数据拟合的模型)分析瞬时变化率,预测下一步趋势。
- 实例:自由落体运动中,已知位移函数 s(t) = 1/2 * gt^2,用微分求瞬时速度 v(t)=s′(t)=gt,即可预测下一时刻物体的速度。
- 实际应用:
- 股票价格预测:用历史数据拟合函数,通过导数预测短期涨跌速率。
- 疫情传播模型:用感染人数函数求导,预测新增病例的变化趋势。
- 积分学的视角:从变化反推原函数(还原过程)
- 核心:已知变化率(如速度、增长率)或变化曲线,结合初始条件(初态),积分还原原函数(如位移、总量)。
- 实例:已知物体速度 v(t)=gt,初始位置 s(0)=0,通过积分 s(t)=∫(0->t)gτ dτ = 1/2 gt^2,还原位移函数。
- 实际应用:
- 经济数据恢复:已知每月GDP增长率,积分还原全年GDP总量。
- 卫星轨道计算:已知加速度(变化率),积分得到速度和位置。
- 关键区别与联系
- 微分:从整体到局部(函数 → 瞬时变化率),用于预测。
- 积分:从局部到整体(变化率 + 初值 → 原函数),用于还原。
- 互为逆运算:微分和积分是微积分基本定理的核心,二者通过初始条件关联。
- 更直观的比喻
- 微分:给你一段录像(连续过程),让你分析某一帧的瞬时动作(如跳水运动员的瞬间速度)。
- 积分:给你一系列快照(每帧的动作变化),让你拼接成完整录像(如通过每秒速度还原跳水全程)。
2、微分学和积分学的桥梁
目前 阿Q 见到的桥梁即为 N-L公式
不定积分 – 可视为函数求导的逆运算(阿Q也可以将其视为微分学范围)
定积分(包括常义定积分和广义定积分 – 反常积分) – 和式极限 (积分学范围)
但是N-L公式成立的前提是非常苛刻的:在所给区间内 ① f(x)可积 ② f(x)原函数存在
几何理解如图:
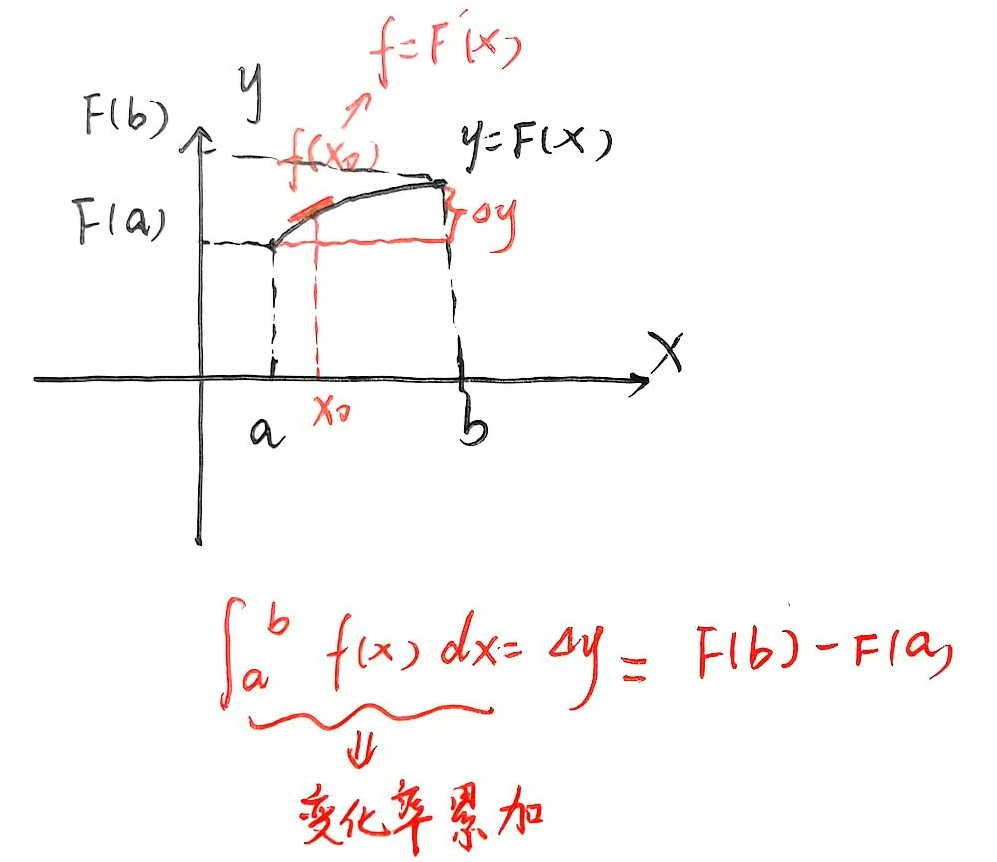
3、不定积分、定积分、反常积分、变限积分的联系和区别:
都需要规定区间范围
1)定积分和反常积分 求出来 都为具体的值,只不过前者要求在有限区间内函数有界,后者是前者的推广(区间有界,函数在区间内有无穷间断点(瑕点) / 区间无界)
2)不定积分 – 求原函数,那就需要保证在 f(x)在区间是连续的
3)变限积分,如变上限积分,其求出的也为函数,只是该函数记录的是从初态到当前位置 f(x)的累加(可理解为原函数变化率的累加)
阿Q:考研复习不仅要会做题,还需要去思考其现实意义 和 概念 (不仅要去学,更要去知道为什么学),这样才能不断提升认知。
25-3-23 定积分应用 – 切片思想
无论是在定积分的几何应用(平面图形的面积、旋转体的体积、平面曲线的弧长、旋转曲面的侧面积、曲边梯形的形心/质心),还是在物理应用(万有引力、液体静压力、变力沿直线做功、抽水做功),都使用到了一种思想 – 切片/微元思想。
以旋转体体积为例,如图:
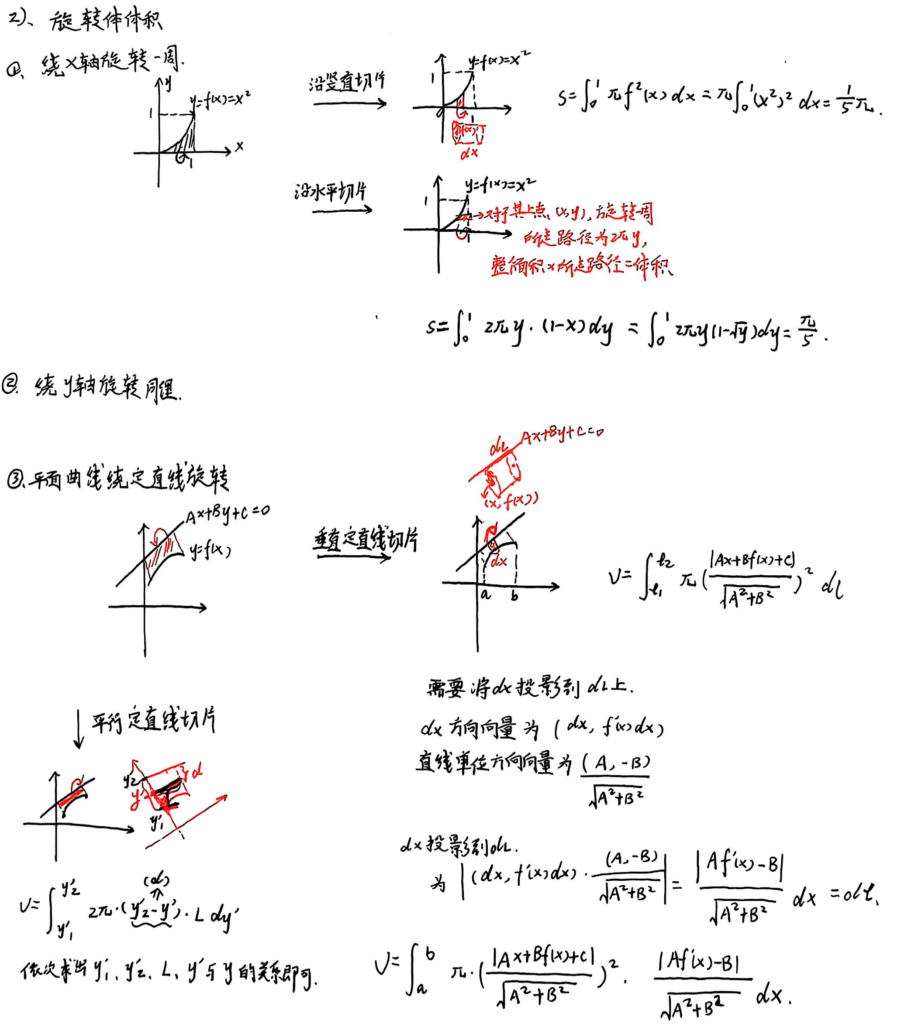
V = (2Π*d) * A,其中 d 为形心到轴的距离,A为平面图形的面积
注意:帕普斯定理的严格条件 – 旋转轴必须位于平面区域所在平面且不能穿过区域内部