图的邻接表存储类似于树存储结构中的孩子表示法。如图：

---

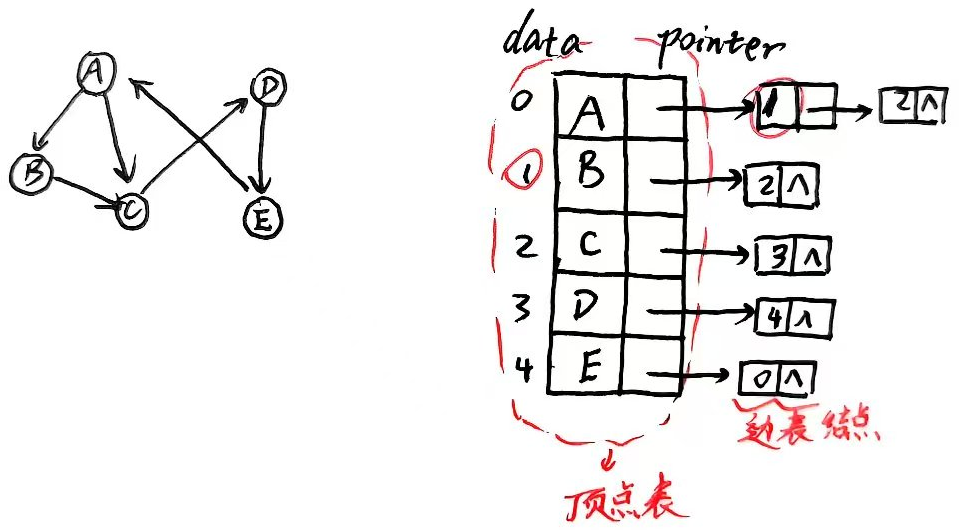
存储类型表示

顶点表结点 数据成员：顶点信息 + 指向下一个邻接边的指针 ；

边表结点 数据成员：当前顶点在顶点表的下标 + 边表指针；

邻接表存图：一维 顶点表结构体数组 + 顶点、边的个数

// 顶点信息
typedef char vetextype;

// 边表结点
typedef struct ArcNode
{
    /* data */
    // 该顶点在顶点表的下标
    int alvex;
    
    // 指向下一个边表结点的指针
    struct ArcNode *next;

    // 若为网，则需要加上权值
    // double Edgeval;
}ArcNode;

// 顶点表结点
#define MaxVexNode 100

typedef struct
{
    /*data*/
    // 顶点信息
    vetextype info;

    // 指向下一个边表结点的指针
    ArcNode *next;
}ALvexNode, AdjList[MaxVexNode]; 

// 邻接表存图
typedef struct
{
    /* data */
    // 顶点表数组
    AdjList Vex;  // 静态分配

    // 顶点个数、边的个数
    int Vexnum, EdgeNum;
}ALGraph;

---

建图过程

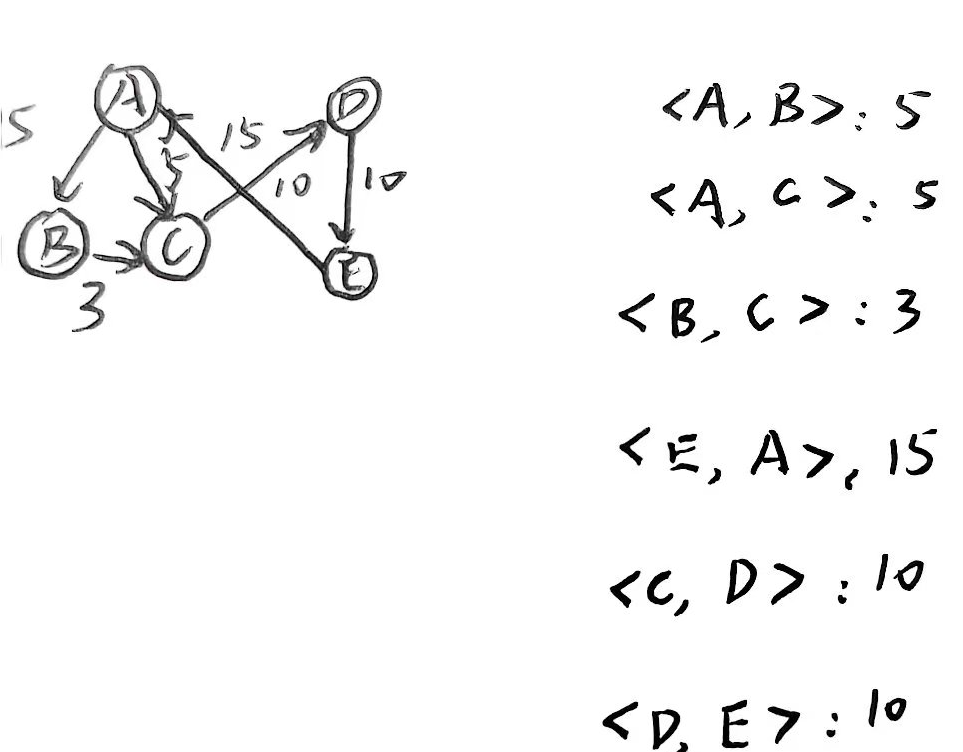
以建立有向网为例

// 建图过程，以建立有向网为例（手动输入顶点信息、边的信息）
#include<iostream>

int FindVex(ALGraph G, vetextype v){
    for(int i = 0; i < G.VexNum; i++)
        if(G.Vex[i].info == v) return i;
    return -1;
}

// 判断<u, v> 存在弧 
bool Exist(ALGraph G, int u, int v){
    ArcNode *ptr = G.Vex[u].next;

    for(; ptr != nullptr; ptr = ptr->next)
        if(ptr->alvex == v) return true;
    
    return false;
}

// 头插法建边表
void CreateGraph(ALGraph &G, int vexnum, int egdenum){
    G.Vexnum = vexnum;
    G.EdgeNum = egdenum;

    // 输入顶点信息
    std::cout << "Input vex info(char): ";
    for(int i = 0; i < G.Vexnum; i++){
        std::cin >> G.Vex[i].info;
        G.Vex[i].next = nullptr;
    }

    int i = 0;
    // 边信息
    while(i < G.EdgeNum){
        // <index1, index2>
        vetextype vex1, vex2;

        // 输入待连接的顶点
        std::cout << "Input vex1 and vex2 info(char): ";
        std::cin >> vex1 >> vex2;

        // 查顶点表，返回坐标
        int index1 = FindVex(G, vex1);
        int index2 = FindVex(G, vex2);

        // 有这俩顶点 且 该边没有存值 才能存入该边的值
        if(index1 == index2 || index1 == -1 || index2 == -1 || Exist(G, index1, index2)){
            std::cout << "Input same Vex / No such Vex / This edge already have value" << std::endl;
            continue;
        }else{
            i++;

            // 新建边表结点
            ArcNode *newArc = new ArcNode;

            std::cout << "Input edgeval: ";
            std::cin >> newArc->Edgeval;

            newArc->alvex = index2;

            // 头插法
            newArc->next = G.Vex[index1].next;
            G.Vex[index1].next = newArc;
        }
    }
}

测试代码

int main(){
    ALGraph G;
    CreateGraph(G, 5, 6);

    // 遍历输出存在边信息
    for(int i = 0; i < G.Vexnum; i++){
        for(ArcNode *ptr = G.Vex[i].next; ptr != nullptr; ptr = ptr->next){
            std::cout << "<" << G.Vex[i].info << "," << G.Vex[ptr->alvex].info << ">" << ": " << ptr->Edgeval << std::endl;
        }
    }
    return 0;
}

/*
输入:
Input vex info(char): ABCDE
Input vex1 and vex2 info(char): AB
Input edgeval: 5
Input vex1 and vex2 info(char): AV
Input same Vex / No such Vex / This edge already have value
Input vex1 and vex2 info(char): AC
Input edgeval: 5
Input vex1 and vex2 info(char): BC
Input edgeval: 3
Input vex1 and vex2 info(char): EA
Input edgeval: 15
Input vex1 and vex2 info(char): CD
Input edgeval: 10
Input vex1 and vex2 info(char): DE
Input edgeval: 10
*/

/*
输出:
<A,C>: 5
<A,B>: 5
<B,C>: 3
<C,D>: 10
<D,E>: 10
<E,A>: 15
*/

---

适用及优劣性

所有类型的图都能存储。【注意：邻接表存储的图不唯一，取决于邻接表算法（头插法/尾插法/…）及边的输入次序】

优点

• 存储空间 O(|V| + （有向图 – 1 或 无向图 – 2）*|E|)，适合存储稀疏图
• 有向图容易计算出度
• 该存储结构下算法实现较为简单

缺点

• 判断给定的顶点间是否存在边/弧 效率低
• 有向图计算入度需要遍历全部邻接表

---

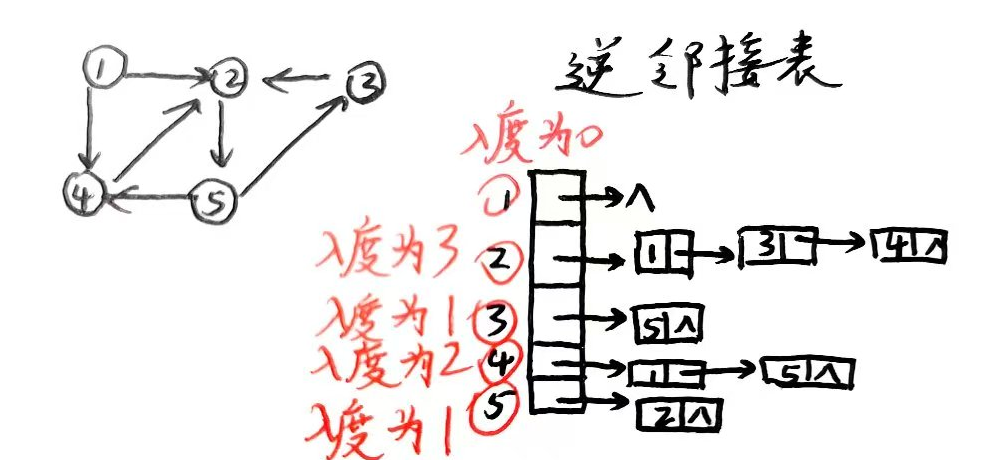
逆邻接表

针对 有向图计算入度需要遍历全部的邻接表 这一劣势，可以用逆邻接表解决。

阿Q：虽然是解决了，但逆邻接表的出度又不容易计算， 那同时用邻接表和逆邻接表存图？