完整代码:堆
逻辑结构
堆是用来干什么的?回答了这个问题,一切都迎刃而解了。
堆被设计出来的目的:
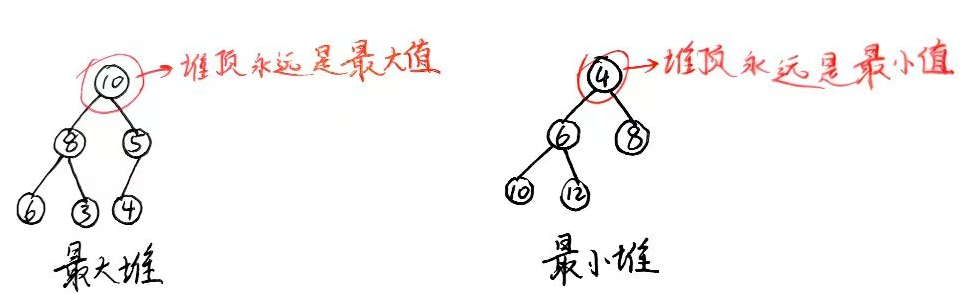
1、堆顶元素永远是最小/最大值
2、从堆尾插入,堆能自动将最小/最大值置于堆顶
这样设计的好处是从堆顶连续取值,永远有序。
那堆可以理解为什么逻辑结构呢?完全二叉树!( 保证结点的标号是连续的,用数组存没有异常值 )
堆主要分为两种类型:
- 最大堆(Max Heap):每个节点的值都大于或等于其子节点的值 -> 能保证堆顶的值是最大的
- 最小堆(Min Heap):每个节点的值都小于或等于其子节点的值 -> 能保证堆顶的值是最小的
如图:
在哈夫曼树存储类型及构造过程中阿Q利用优先队列快速建链式哈夫曼树,这其实就用到了最小堆。
存储类型表示
既然是完全二叉树,那就用数组存咯(顺序存储),链式也不是不行,只不过较为麻烦。
// 结点
typedef struct
{
int val; // 结点比较的值
// 可能还有其他数据成员
}HeapNode;
// 堆
#define MAXNODE 100
typedef struct
{
/* data */
HeapNode node[MAXNODE];
int size; // 记录结点个数
}Heap;操作
基本操作 – 上浮 & 下沉 (下列代码为实现最小堆,最大堆同理)
下列为了代码更简洁 (也更专注于操作本身),阿Q默认结点内只有 val 值
typedef struct
{
int val[MAXNODE];
int size;
}Heap;// 交换操作
void swap(int &val1, int &val2){
int tmp = val1;
val1 = val2;
val2 = tmp;
}初始化
// 初始化
void InitHeap(Heap &H){
H.size = 0;
}上浮(时间复杂度O(logn)1)
上浮过程如下图:
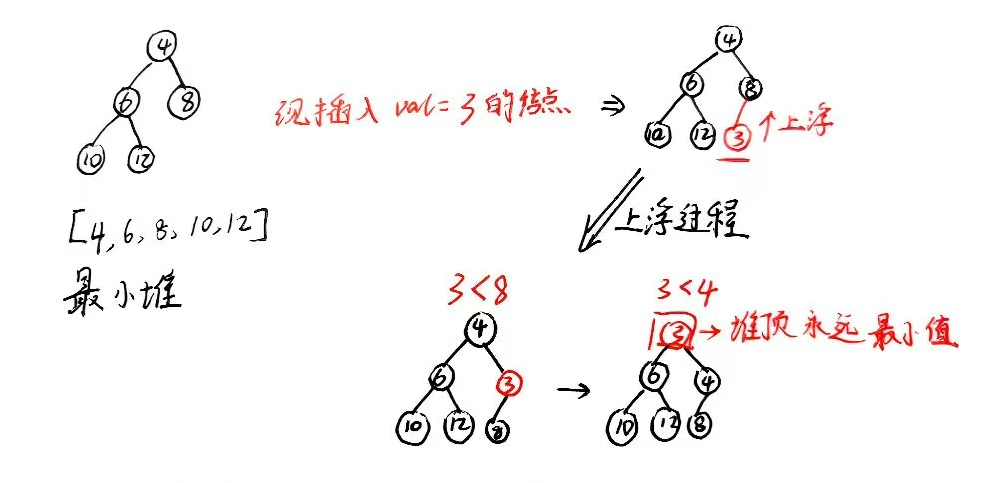
void heapifyup(Heap &H, int index){
// 沿双亲进行比较
int ptr = index;
while(ptr != 0){
int parent = (ptr - 1) >> 1;
if(H.val[parent] > H.val[ptr]) swap(H.val[parent], H.val[ptr]);
// 否则上浮结点已处于正确位置,退出循环即可
else break;
ptr = parent;
}
}插入
从数组尾插入,再进行上浮即可。
void insertHeap(Heap &H, int val){
if(H.size == MAXNODE){
std::cout << "The Heap is full" << std::endl;
return;
}
// 数组尾插入
H.val[H.size] = val;
// 上浮操作
heapifyup(H, H.size);
H.size++;
}
下沉 (时间复杂度O(logn))
下沉过程如图:
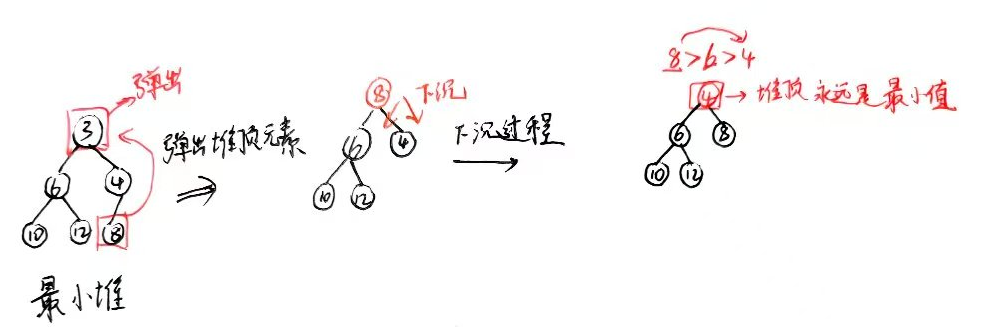
void heapifydown(Heap &H, int index){
// 沿孩子进行比较
int ptr = 2 * index + 1;
while(ptr < H.size){
int parent = (ptr - 1) >> 1;
// 与孩子中最小的结点进行比较
if((ptr + 1) < H.size && H.val[ptr] > H.val[ptr+1]) ptr = ptr + 1;
if(H.val[parent] > H.val[ptr]) swap(H.val[parent], H.val[ptr]);
// 否则下称结点已处于正确位置,退出循环即可
else break;
ptr = 2 * ptr + 1;
}
}弹出堆顶元素
弹出堆顶元素,那从数组的哪个位置的元素移到堆顶呢? 仍然是数组尾
// 弹出堆顶元素
void PopHeap(Heap &H){
if(H.size == 0){
std::cout << "The Heap is empty" << std::endl;
return;
}
H.val[0] = H.val[H.size - 1];
H.size--;
heapifydown(H, 0);
}查堆顶
// 查堆顶
int heapTop(Heap H){
return H.val[0];
}堆化
将一个无序的数组转化为堆结构;有两种方案:
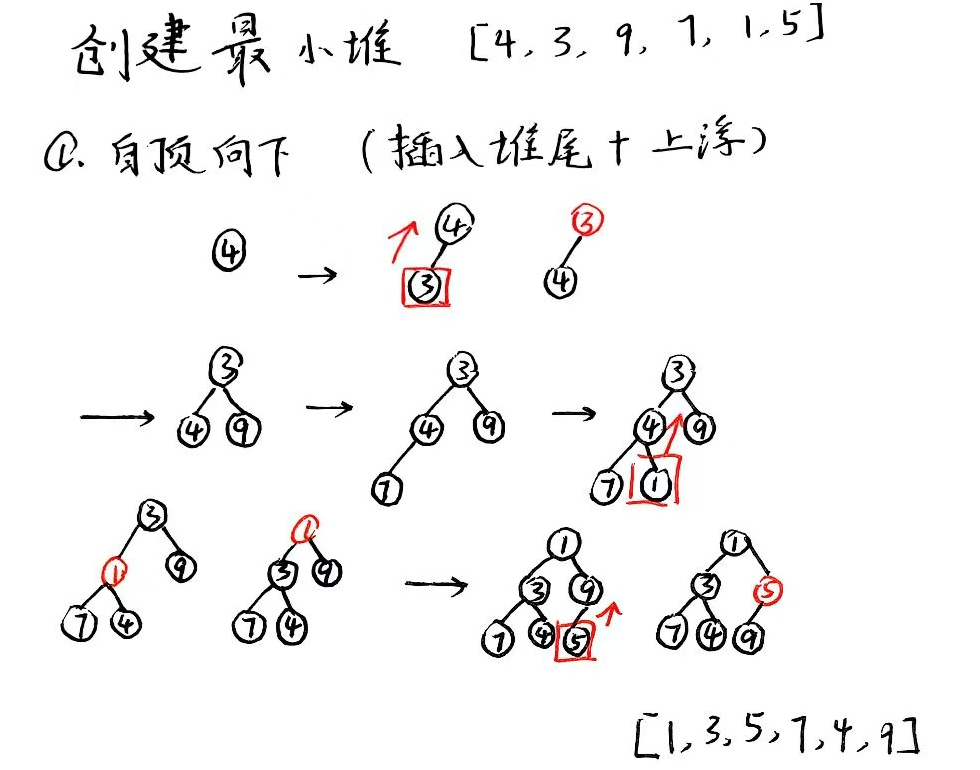
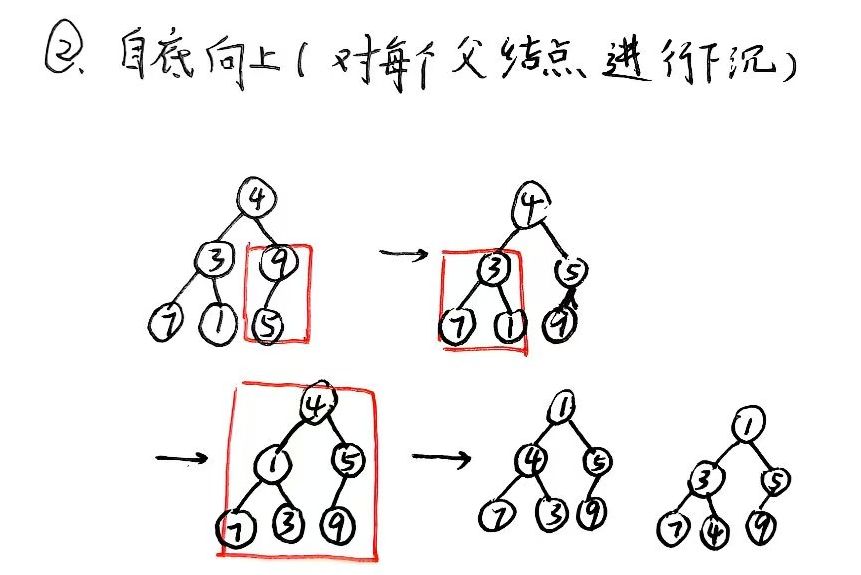
// 自顶向下
Heap TopCreateHeap(int val[], int n){
Heap H;
InitHeap(H);
// 插入堆尾 + 上浮
for(int i = 0; i < n; i++)
insertHeap(H, val[i]);
return H;
}// 自底向上
Heap DownCreateHeap(int val[], int n){
Heap H;
InitHeap(H);
for(int i = 0; i < n; i++){
H.val[i] = val[i];
}
H.size = n;
// 对每个父节点下沉
int parent = (n - 1 - 1) >> 1;
for(int i = parent; i > -1; i--)
heapifydown(H, i);
return H;
}测试代码
#include"heap.h"
#define n 6
int main(){
int val[n] = {4, 3, 9, 7, 1, 5};
std::cout << "Top-Down Approach" << std::endl;
Heap H1 = TopCreateHeap(val, n);
for(int i = 0; i < H1.size; i++){
std::cout << H1.val[i] << " ";
}
std::cout << std::endl << "Down-Top Approach" << std::endl;
Heap H2 = DownCreateHeap(val, n);
for(int i = 0; i < H2.size; i++){
std::cout << H2.val[i] << " ";
}
return 0;
}
/*
输出结果:
Top-Down Approach
1 3 5 7 4 9
Down-Top Approach
1 3 5 7 4 9
*/应用
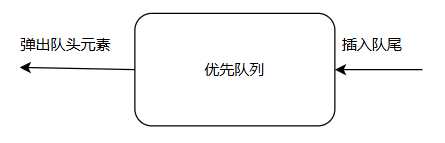
优先队列
前文已经提到,阿Q在创建链式哈夫曼树时用到了优先队列。
优先队列的操作仅有 ①插入队尾 – 自动上浮;②弹出队头元素 – 自动下沉
最大堆 -> 依次弹出后的元素从大到小排序
最小堆 -> 依次弹出后的元素从小到大排序 (链式哈夫曼树构造选择)
int main(){
// 优先队列原理
Heap PriorQueue;
InitHeap(PriorQueue);
int num;
std::cout << "input num of values: ";
std::cin >> num;
int val;
for(int i = 0; i < num; i++){
std::cout << "Input n." << i + 1 << " value: ";
std::cin >> val;
insertHeap(PriorQueue, val);
}
// 依次弹出队头元素 (从小到大)
while(PriorQueue.size != 0){
std::cout << heapTop(PriorQueue) << " ";
PopHeap(PriorQueue);
}
return 0;
}
/*
输入:
input num of values: 6
Input n.1 value: 4
Input n.2 value: 3
Input n.3 value: 9
Input n.4 value: 7
Input n.5 value: 1
Input n.6 value: 5
输出结果:
1 3 4 5 7 9
*/堆排序
上面阿Q已经实现了连续弹出的元素即为排序的结果。
堆排序 是在原本的堆内进行排序,那这个过程是怎样进行的呢?看下图:
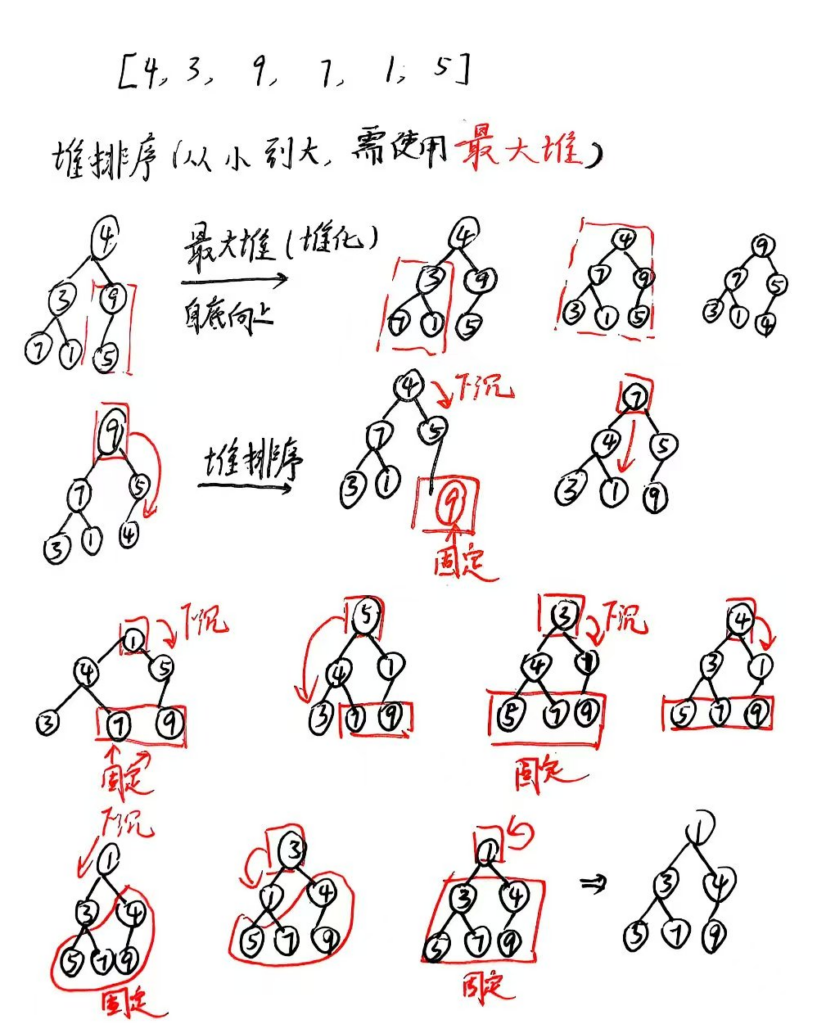
同理,若要实现从大到小排序,需要先将数组转化为最小堆,然后再进行堆排序
// 之前阿Q实现了最小堆
// 因此此处实现从大到小的堆排序
void Sort_largest_to_smallest(Heap &H){
int n = H.size;
// 维护与堆顶待交换的位置 (注意:此处应将H的 size更改,否则固定的数组区域会被更改)
H.size--;
while(H.size > 0){
swap(H.val[0], H.val[H.size]);
// 堆顶结点下沉
heapifydown(H, 0);
H.size--;
}
H.size = n;
}
Heap HeapSort(int val[], int n){
// 要堆化为最小堆
Heap H = DownCreateHeap(val, n);
// 进行堆排序
Sort_largest_to_smallest(H);
return H;
}测试代码
#define n 6
int main(){
int val[n] = {4, 3, 9, 7, 1, 5};
Heap H = HeapSort(val, n);
// 打印
for(int i = 0; i < H.size; i++){
std::cout << H.val[i] << " ";
}
return 0;
}
/*
输出结果:
9 7 5 4 3 1
*/图算法应用
动态中位数
核心作用:通过两个堆动态平衡数据流,快速获取中位数。
问题场景
- 数据流持续输入,需实时返回当前所有数据的中位数。
- 直接排序每次插入需
O(n),效率低
解决: 双堆法(最大堆 + 最小堆)
- 结构设计:
- 最大堆:保存较小的一半数据,堆顶为最大值。
- 最小堆:保存较大的一半数据,堆顶为最小值。
- 平衡条件:两堆大小差不超过1。
- 操作步骤:
- 新元素插入:
- 若元素 ≤ 最大堆顶,插入最大堆;否则插入最小堆。
- 平衡堆大小:
- 若最大堆比最小堆多2个元素,将最大堆顶移到最小堆(多一个元素那说明平均值就为最大堆的堆顶)
- 若最小堆比最大堆多1个元素,将最小堆顶移到最大堆
- 获取中位数:
- 若两堆大小相等,中位数为两堆顶的平均值
- 否则,中位数为较大堆的堆顶(按平衡堆大小方案,较大堆只能在最大堆中,即直接取最大堆的堆顶即可)
- 新元素插入:
- 时间复杂度:每次插入
O(log n),查询中位数O(1)。
过程如图:
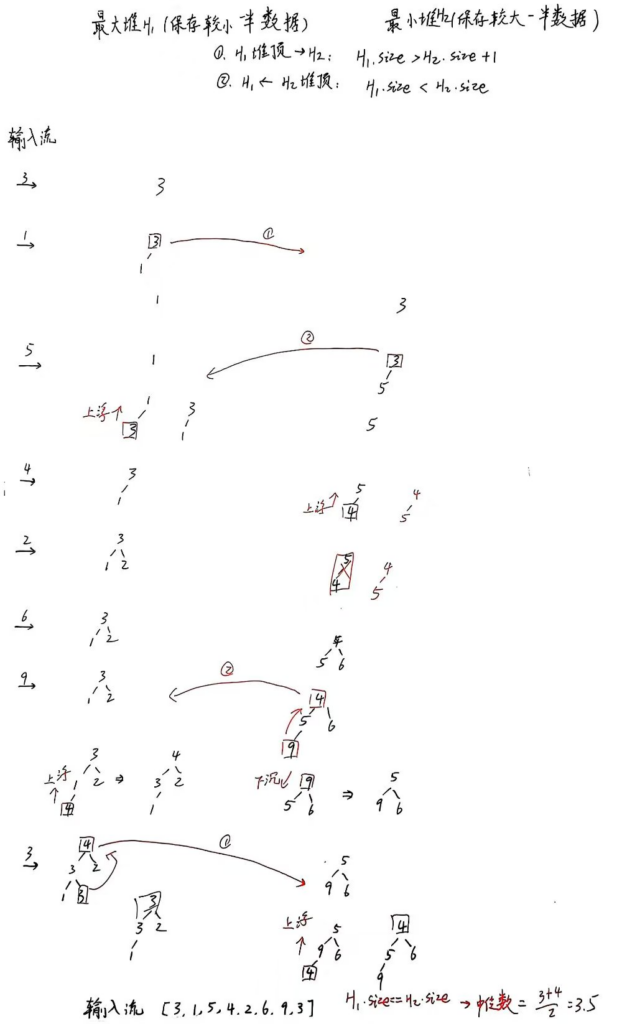
2)H1堆顶元素插入H2:H1.size > H2.size + 1;H2堆顶元素插入H1:H1.size < H2.size
3)最终:若 H1.size == H2.size,中位数则为两堆顶值的平均数;若H1.size > H2.size,中位数为H1堆顶值
事件驱动模拟
核心作用:按时间顺序处理事件,高效调度未来事件
问题场景
- 模拟离散事件(如银行排队、网络数据包传输),事件按时间顺序触发。
- 需按时间顺序处理事件,并在处理过程中生成新事件。
事件调度实现
- 堆的用途:最小堆按事件发生时间排序,堆顶总是下一个最早事件。
- 步骤:
- 初始化:将所有初始事件(如客户到达)插入堆。
- 循环处理:
- 取出堆顶事件(时间最早)。
- 处理事件,可能生成新事件(如客户离开)插入堆。
- 示例(银行排队):
- 事件类型:
到达(时间,客户)、离开(时间,柜台) - 初始事件:
到达(10:00, 客户A)、到达(10:05, 客户B) - 处理
到达(10:00, 客户A):- 分配柜台,生成
离开(10:07, 柜台1)插入堆。
- 分配柜台,生成
- 处理
到达(10:05, 客户B):- 若柜台忙,加入队列,否则生成离开事件。
- 事件类型:
- 时间复杂度
- 插入和删除事件均为
O(log n),n为待处理事件数。
- 插入和删除事件均为
- 完全二叉树中有n个结点,则树高为⌊log2n⌋ + 1 ↩︎